Les bases

Si vous ne possédez pas déjà de système de points et que vous ne savez pas par où commencer, nous vous suggérons de commencer avec l’un de nos systèmes de points prédéfinis (Logarithmique, Racine carrée, Linéaire):

Vous pouvez les tester et voir l’attribution de points pour un tournoi type à droite de l’écran de création de championnat

Fixe

L’option Fixe vous offre un peu de personnalisation avec l’interface ci-dessus:

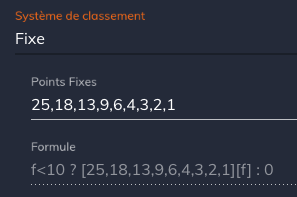
Dans cet exemple les points suivants seront attribués:

• 1ère place: 25 points,
• 2ème place: 18 points,
• 3ème place: 13 points,
• etc.

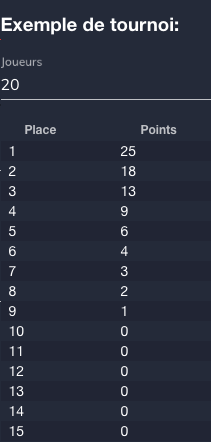
Vous pouvez modifier la liste des points et vous pouvez voir les points changent. Vous pouvez changer le nombre de joueurs pour le tournoi exemple à droite pour verifier que ça fonctionne comme vous voulez:

Système personnalisés

Le système qui nous intéresse vraiment pour cet article est l’option « Personnalisé » ou vous pouvez créer votre propre système de points.

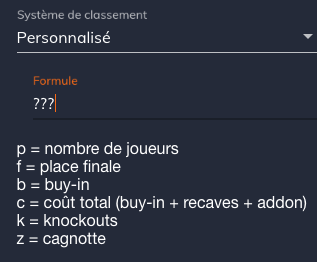
Cet image montre les différent variables disponible pour vos formules

Certains s’appliquent au tournoi global:

• p = nombre de joueurs
• b = buy-in
• z = cagnotte

et certains s’appliquent au joueur individuel

• f = place finale
• c = coût total (buy-in + recaves +  addons)
• k = knockouts

Exemples

Linéaire

Si vous choisissez l’option « Linéaire » vous pouvez voir la formule utilisée:

p-f+1

Donc, si un joueur termine 5ème sur 30 joueurs, il recevra 26 points (30 – 5 + 1)

Fixe

Nous pouvons voir un exemple que la formule « Fixe » ci-dessous:

f <10? [25,18,13,9,6,4,3,2,1] [f]: 0

Cela a l’air complexe mais ça veut dire, simplement:

Si le joueur termine meilleur que la 10ème place:

Attribuez des points de cette liste [25,18,13,9,6,4,3,2,1], si f = 3 donnez-moi le 3éme de la liste, si f = 5 donnez-moi le 5éme de la liste, etc.

Sinon, donnez 0 points

 

Linéaire avec un bonus pour le gagnant

Que faire si nous voulons utiliser une formule « linéaire » mais donner un bonus de 5 points au gagnant?

Dans ce cas, nous pouvons utiliser une expression conditionnelle:

X ? Y: Z

Ce qui peut être lu comme « Si X alors Y, sinon Z »

Donc pour notre exemple, ce serait:

p-f + 1 + (f == 1? 5: 0)

Il s’agit donc d’un système de points linéaires standard auquel vous ajoutez ensuite le bonus « si la position finale == 1, donne 5 points bonus, sinon 0 points bonus »

Remarque: utilisez toujours le signe double égal « == » pour comparer deux valeurs.

Points fixes pour le top 3 et 1 point de participation pour les autres

Dans cet exemple, nous allons attribuer des points comme:

1ère place: 10 points
2éme place: 7 points
3ème place: 4 points
Tous les autres: 1 point
Nous pouvons donc utiliser ici la fonction fixe légèrement modifiée:

f <4? [10,7,4] [f]: 1

Ce qui pourrait se lire comme: « Si le joueur termine mieux que 4ème, attribuez 10,7 points ou 4 points, sinon attribuez un point »

À peu près tout système de points peut être modélisé avec une formule personnalisée. Essayez-le et faites-nous savoir si vous êtes bloqué, nous serons heureux de vous aider à trouver la formule qui convient à votre championnat: support@blindvalet.com

Reference

Operators

Operator	Name	Syntax	Associativity	Example	Result
+	Add	x + y	Left to right	4 + 5	9
-	Subtract	x - y	Left to right	7 - 3	4
*	Multiply	x * y	Left to right	2 * 3	6
/	Divide	x / y	Left to right	6 / 2	3
%, mod	Modulus	x % y	Left to right	8 % 3	2
^	Power	x ^ y	Right to left	2 ^ 3	8
!	Factorial	y!	Left to right	5!	120
? :	Conditional expression	x ? y : z	Right to left	15 > 100 ? 1 : -1	-1
:	Range	x : y	Right to left	1:4	[1,2,3,4]
==	Equal	x == y	Left to right	2 == 4 - 2	true
!=	Unequal	x != y	Left to right	2 != 3	true
<	Smaller	x < y	Left to right	2 < 3	true
>	Larger	x > y	Left to right	2 > 3	false
<=	Smallereq	x <= y	Left to right	4 <= 3	false
>=	Largereq	x >= y	Left to right	2 + 4 >= 6	true

Constants

Constant	Description	Value
e, E	Euler’s number, the base of the natural logarithm.	2.718281828459045
LN2	Returns the natural logarithm of 2.	0.6931471805599453
LN10	Returns the natural logarithm of 10.	2.302585092994046
LOG2E	Returns the base-2 logarithm of E.	1.4426950408889634
LOG10E	Returns the base-10 logarithm of E.	0.4342944819032518
NaN	Not a number.	NaN
null	Value null.	null
phi	Phi is the golden ratio. Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Phi is defined as (1 + sqrt(5)) / 2	1.618033988749895
pi, PI	The number pi is a mathematical constant that is the ratio of a circle’s circumference to its diameter.	3.141592653589793
SQRT1_2	Returns the square root of 1/2.	0.7071067811865476
SQRT2	Returns the square root of 2.	1.4142135623730951
tau	Tau is the ratio constant of a circle’s circumference to radius, equal to 2 * pi.	6.283185307179586

Functions

Function	Description
abs(x)	Calculate the absolute value of a number.
cbrt(x [, allRoots])	Calculate the cubic root of a value.
ceil(x)	Round a value towards plus infinity If x is complex, both real and imaginary part are rounded towards plus infinity.
cube(x)	Compute the cube of a value, x * x * x.
exp(x)	Calculate the exponent of a value.
expm1(x)	Calculate the value of subtracting 1 from the exponential value.
fix(x)	Round a value towards zero.
floor(x)	Round a value towards minus infinity.
log(x [, base])	Calculate the logarithm of a value.
log10(x)	Calculate the 10-base logarithm of a value.
log1p(x)	Calculate the logarithm of a value+1.
log2(x)	Calculate the 2-base of a value.
mod(x, y)	Calculates the modulus, the remainder of an integer division.
nthRoot(a)	Calculate the nth root of a value.
nthRoots(x)	Calculate the nth roots of a value.
pow(x, y)	Calculates the power of x to y, x ^ y.
round(x [, n])	Round a value towards the nearest integer.
sign(x)	Compute the sign of a value.
sqrt(x)	Calculate the square root of a value.
square(x)	Compute the square of a value, x * x.
and(x, y)	Logical and.
not(x)	Logical not.
or(x, y)	Logical or.
xor(x, y)	Logical xor.
random([min, max])	Return a random number larger or equal to min and smaller than max using a uniform distribution.
randomInt([min, max])	Return a random integer number larger or equal to min and smaller than max using a uniform distribution.
mad(a, b, c, …)	Compute the median absolute deviation of a list with values.
max(a, b, c, …)	Compute the maximum value of a list with values.
mean(a, b, c, …)	Compute the mean value of a list with values.
median(a, b, c, …)	Compute the median of a list with values.
min(a, b, c, …)	Compute the maximum value of a list of values.
mode(a, b, c, …)	Computes the mode of a set of numbers or a list with values(numbers or characters).
prod(a, b, c, …)	Compute the product of a list with values.
std(a, b, c, …)	Compute the standard deviation of a list with values.
sum(a, b, c, …)	Compute the sum of a list with values.
var(a, b, c, …)	Compute the variance of a list with values.
acos(x)	Calculate the inverse cosine of a value.
acosh(x)	Calculate the hyperbolic arccos of a value, defined as acosh(x) = ln(sqrt(x^2 - 1) + x).
acot(x)	Calculate the inverse cotangent of a value, defined as acot(x) = atan(1/x).
acoth(x)	Calculate the hyperbolic arccotangent of a value, defined as acoth(x) = atanh(1/x) = (ln((x+1)/x) + ln(x/(x-1))) / 2.
acsc(x)	Calculate the inverse cosecant of a value, defined as acsc(x) = asin(1/x).
acsch(x)	Calculate the hyperbolic arccosecant of a value, defined as acsch(x) = asinh(1/x) = ln(1/x + sqrt(1/x^2 + 1)).
asec(x)	Calculate the inverse secant of a value.
asech(x)	Calculate the hyperbolic arcsecant of a value, defined as asech(x) = acosh(1/x) = ln(sqrt(1/x^2 - 1) + 1/x).
asin(x)	Calculate the inverse sine of a value.
asinh(x)	Calculate the hyperbolic arcsine of a value, defined as asinh(x) = ln(x + sqrt(x^2 + 1)).
atan(x)	Calculate the inverse tangent of a value.
atan2(y, x)	Calculate the inverse tangent function with two arguments, y/x.
atanh(x)	Calculate the hyperbolic arctangent of a value, defined as atanh(x) = ln((1 + x)/(1 - x)) / 2.
cos(x)	Calculate the cosine of a value.
cosh(x)	Calculate the hyperbolic cosine of a value, defined as cosh(x) = 1/2 * (exp(x) + exp(-x)).
cot(x)	Calculate the cotangent of a value.
coth(x)	Calculate the hyperbolic cotangent of a value, defined as coth(x) = 1 / tanh(x).
csc(x)	Calculate the cosecant of a value, defined as csc(x) = 1/sin(x).
csch(x)	Calculate the hyperbolic cosecant of a value, defined as csch(x) = 1 / sinh(x).
sec(x)	Calculate the secant of a value, defined as sec(x) = 1/cos(x).
sech(x)	Calculate the hyperbolic secant of a value, defined as sech(x) = 1 / cosh(x).
sin(x)	Calculate the sine of a value.
sinh(x)	Calculate the hyperbolic sine of a value, defined as sinh(x) = 1/2 * (exp(x) - exp(-x)).
tan(x)	Calculate the tangent of a value.
tanh(x)	Calculate the hyperbolic tangent of a value, defined as tanh(x) = (exp(2 * x) - 1) / (exp(2 * x) + 1).